Equations of Motion for Rocket
In order to derive the equations of motion of a rocket the book Introduction to Space Dynamics did a poor job explaining why things work out the way they are derived. Instead I will be using a technique called control volume analysis to derive the equations of motion for the rocket. Control volume analysis is a technique that basically converts newtons equations into a system that is ideally suited for fluids. So instead of point masses, we would be dealing with mass flow rates. In particular we will be using the conservation of linear momentum to derive the equation of motion for a rocket.
The Linear Momentum Equation
The linear momentum equation is simply stated as:
m is the mass of the rocket which is changing in time. V is the velocity of the fluid escaping the rocket. rho is the density of the fluid. A key point in here is that V is the velocity in the inertial frame of reference. I will not derive how newton’s equation got into this form. Perhaps check out a fluid mechanics book such as Fluid Mechanics by Frank M. White.
Normally we know what is the velocity of the fluid escaping the rocket in the moving frame of reference of the rocket. This means we have to readjust formula 1 above to take into account the inertial forces due to the moving frame of reference.
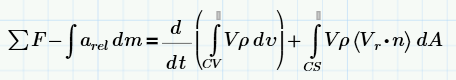
This equation can then be simplified by assuming a one dimension solution as shown below.
We finally arrive to the final equation:
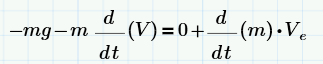
Of all these variables we need to explore the velocity of the fluid escaping the rocket. The velocity of such a fluid is dependent on the chemical properties of the propellant. Per Thomson, “for chemical propellants, the ejection speed u relative to the rocket nozzle depends on the heat energy per pound which must be high, and on the molecular weight which must be small. Its performance is rated by the specific impulse I, defined as the thrust of a pound of propellant multiplied by the number of seconds required to burn it.”. The relationship between velocity and specific impulse is u=gI = 32.2I ft/s.
Here are some examples of Specific Impulse (check out Wikipedia or other sources for more info):
- Ammonium nitrate rubber (Solid) 170-210
- Potassium perchlorite thickol or asphalt (Solid) 170-210
- Boron metal components and oxidant (Solid) 200-250
- Liquid Oxygen alcohol 250-270
- Liquid Oxygen fluorine JP4 270-330
- Fluorine Hydrogen 300-385
- Liquid Oxygen and Hydrogen 450
What I like about the Thompson book, is that it goes to present some analytical formulas that show what is the expected performance of single stage rocket. I will show some of those in the following sections.
Analytical Formulas
We should define a parametric parameter called the thrust ratio. The thrust ratio is the thrust of the rocket divided by the initial mass of the rocket. R=T/(mo*g). From the equation relating thrust and mass rate and gas velocity, we find that the duration of the powered flight is:
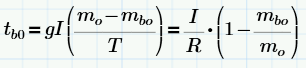
tbo is the final time at burn out. mo is the initial mass of the rocket. mbo is the final mass of the rocket at burnout. T is the thrust of the rocket. I is the specific impulse. g is the gravitational constant of earth. Now from formula 3, we can find the maximum achievable velocity of the rocket by integrating the formula.
Substituting formula 4 into formula 5 we get:
Now we can plot the final velocity as a function of the mass ratio, specific impulse, and thrust ratio. A little knowledge of rocket configuration will come in handy when selecting realistic values.
Final Velocity of Single Stage Rockets
A plot for formula 6 is shown below. As expected we are able to achieve a higher velocity if the ratio between the payload mass and the initial rocket mass is small. Higher specific impulse will improve our ability to reach higher velocities and higher thrust ratios will also help us.
Per Thompson however, current technology prevents us from achieving mass ratios less than 0.1. In order to achieve say orbital velocity around the earth, we need to be flying at speeds of 25,000 ft/s. This is not an apples to apples comparison since the previous analysis simplified a bunch of stuff. For example we assumed the rocket is always being pulled by gravity. Or that there are no aerodynamic forces. Nonetheless, as seen from the plot above, we are not able to achieve such high velocities if the mass ratio is larger than 0.1. In order to get to orbital type velocities, our thrust ratio has to be higher than 2 or our specific impulse must be larger than 350.
This is why no one (at least for now) uses single stage to orbit rockets. It is just too darn hard and why bother when multi-stage rockets do pretty well. That is where I will be heading next, going over why multistage rockets help us so much.
Rocket Sim 